高速化できる最小費用流のよくあるからくり / グリッド上の最大流問題
この記事は Competitive Programming (1) Advent Calendar 2019 - Adventar の25日目の記事です.
24日目はbeet_aizuさんの記事で,Online Judge Verify Helper のススメ - beet's soilでした.
この記事ですが,気合を入れすぎたので15ページもあります.
その分,短い記事ではフォローすることが難しい概念を説明したつもりですので,お楽しみください.
イントロ
この記事は次のとおり,二部構成となっています.
前半は「普通に考えると最小費用流なのに$O(N)$や$O(N \log N)$程度の計算量を要求されてしまう...」という類の問題についてです.この問題へのアプローチと例題の解説をします.
紹介する問題 : JOI2018/2019 本選 問題4「コイン集め」
後半は「グリッド上の最大流」になります.左上から右下へ容量無限大の辺を無数に張られていて,ソースとシンクがたくさんあるような設定の最大流について扱います.
紹介する問題 : いろはちゃんコンテストDay4 F「道なき道を」, JOI2018/2019 春合宿 Day2 「ふたつの料理」
想定読者層は,最大流問題,最小費用流問題について,それぞれ問題を解いたことがあるのが最低ラインだと思います.(特に何の理由もつけずに,「この問題はナイーブなフローで解けますね~」,くらいの説明をすることになります)
本編
tokoharupage/advent2019.pdf at master · tokoharu/tokoharupage · GitHub
手元にダウンロードして読むのがよいかと思います

modint構造体の工夫
(注 (2021/1/31) : この記事はとても古く、なおかつもっといい実装が考えられます。さらに言えば、AtCoderではac-libraryが整備されている現在では価値は無いと思われます)
はじめに
プログラミングコンテストの問題では、答えをある値で割ったあまりを求める問題が頻出ですが、バグを生じやすい特徴があります。その例は次の記事の序文に詳しく記述されています。
noshi91.hatenablog.com
この記事では、C++においてこの種の問題を解決するための対策として、modint構造体を導入しました。これにより、本質的な式の記述に集中することができるようになるなど、多くの利点を享受することができます。
しかし、次の欠点があることにも触れられています
- 実行時にMODの値が決定する場合は使用不可。代わりに別の実装を用いる必要がある。
- アルゴリズムに依存した高速化 : 例えば 「+= (intの範囲の数)」を行いたいときに途中でMODを取ることは時間の無駄ですが、そのチューニングが難しくなる
今回の記事では、これらの欠点をそれなりに克服するmodint構造体を紹介します。
コンセプト
具体的な演算を除いたメイン部分のコードを示します。
vector<long long> MODS = {998244353}; template <int kind = 0, int fast = 0> class mint { public: long long v; mint() : v(0) {} mint(long long v) : v(fast == 0 ? (v < 0 ? (v % MODS[kind] + MODS[kind]) % MODS[kind] : (v >= MODS[kind] ? v % MODS[kind] : v)) : (v)) {} long long get_mod() { return MODS[kind]; } long long get_val() { return v; } void take_mod() { v %= MODS[kind]; } };
実行時にMODを指定する
特徴の一つはMODの値を可変値にすることです。この指定方法は途中で値に変更があると計算が壊れてしまう可能性があるという意味で優れたコードだとは言えません。しかしながら、実行時にMODを指定できるようにしたいため、このような書き方になりました。(もっときれいな書き方があるとは思いますので、あれば是非教えてください。)
テンプレート引数kindの初期値は0ですので、mint<>の宣言でデフォルト値のMODでのmodint型を宣言できます。また、ほかのMOD値を使用したい場合にはvectorコンテナMODSへ要素を追加し、mint<1>などの宣言をすれば使用できます。
また、一般にテンプレートを使用するメリットとして、異なるテンプレート値を持つオブジェクトの間の演算をコントロールできる点が挙げられます。
例えばmodint構造体では、積のような演算は同じMOD値でのみ行いたいという自然な要請があるため、異なるMOD値を持つオブジェクトどうしの演算はコンパイルエラーで弾いてほしいものです。これを実現するために、積の演算は次のように記述しています。
template <int kind> mint<kind>& operator*=(mint<kind>& a, mint<kind> b) { return a = a.v * b.v; }
これで同じMOD値(より正確にはテンプレートパラメータkindの値)どうしの演算でなければコンパイルエラーが発生することになり、誤答を未然に防ぐことができます。
また、同じMOD値でも本質的に混ぜてはいけなければ、同じMOD値を用いつつテンプレートパラメータkindを変えてもよいかもしれません(が、そんなことが必要な状況に出会ったことはありません)
最後に、コード例として、Educational DP Contestの問題S - Digit Sumへの提出Submission #5077234 - Educational DP Contestを紹介します。
この問題では数え上げに対するMOD値とDPのindexに関するMOD値の二つのMOD値を扱います。また、indexに関するMODは実行時に与えられています。先ほど紹介したコードではこれらを共通のクラスで処理出来ていることがわかります。
高速化オプション
次に、高速化オプションについて説明します。冒頭のコードのテンプレートパラメータにfastというものがありました。これは0のときは通常モードで、1のときはMOD演算をスキップすることで多少の高速化を行うモードであることを表しています。(現状テンプレートパラメータの型がintになっていますが、boolにする方がよさそうですね)
このパラメータを導入する理由は、冒頭でも説明した通り、intの範囲に収まる加算のみを行う場合には、速度を考慮に入れるとMODを取る回数を少なくしたい場合があるからです。
実際の例を紹介します。天下一プログラマーコンテスト2019の問題
F - Banned Xへの、fastパラメータをOFFにしている提出
Submission #5078264 - Tenka1 Programmer Contest 2019(341ms)
とONにしている提出
Submission #5074374 - Tenka1 Programmer Contest 2019(265ms)
です。
さて、この二つのコードの相違は"mint<> ans = 0;"と"mint<0, 1> ans = 0;"の違いのみです。したがって、この方針のメリットとして、一度プログラムがTLEしてしまった場合に、大規模な修正をかけることなく、演算手法を指定することができる点が挙げられます*1。
今回できていないこと
他の方に教えていただきましたが、コンパイラに定数であることが伝わっていればMOD演算が高速になります。
そこをサポートできるとよりよさそうです。
まとめ
- modint構造体に対する2点の工夫を紹介しました
- 実行時にMOD値を指定する
- 高速化オプションのパラメータを加える
- 書き方はまだ改善ができそうに感じています
- より良い書き方があればぜひ教えてください
*1:なお、このコードではfast=1に対する演算は加算しかサポートしていません。減算にも対応しているとよいなぁ、と書いている途中に思いました
競技プログラミング再入門 環境構築編
はじめに
私は競技プログラミングでは、5年くらい前に頑張っていた時期がありましたが、最近は気が向いたらコンテストに出るくらいでした。ところが、さすがにそれだと問題が生じてきました。
- 昔整備したライブラリは滅茶苦茶なまま。何がどこに行ったかわからない。
- 最近のエディタについていけていない
そこで色々とリフォームをしようと思い、主にこの土日で頑張りました。今回はそれを記録しておこうと思います。
タイトルにある「再入門」は、今まで惰性で競技プログラミングに関わっていたところを、もう少しまじめに取り組もうという気持ちがあるのでつけました。ぼちぼち頑張っていこうと思います。
今回の環境
各種設定にあたっては、次の記事を大きく参考にしました。この場で感謝いたします。
Visual Studio Codeで競プロ環境構築 - Qiita
atcoder-toolsの設定
コンテストに出ての感想
- atcoder-toolsは最高
- REが出たときにprintデバッグできないのが惜しい?
- サクッとデバッガを使えるようにしろという話な気がする
- printデバッグばかりをした。dump関数は便利。
- cpplintちょっとうっとうしいかも
- 結局Warning全然見なかった
- ノリで変数をたくさん宣言していたので、UnusedVariableがたくさん出ることは目に見えていたのがあるかも?
- どう運用していくのがいいかな...
- snipetも用意した分は全然使わなかった
- これはまだまだ未完成なので少しずつ拡張していきたい。
- グラフとか木に対するデバッグ出力が欲しくなった
- Indentation Level Movement あたりは全然使わなかった。
- これは意識的に慣れないとどうしようもなさそう
次にやりたいこと
Snipet, ライブラリまわりは改善のやりようがあるからこのあたりをやりたい。
また、結構設定が多くなりそうなので、できる限りgitで管理しようと思う。
今回は特に触れなかったが、考察の粗は何とかしたい。これはAnkiあたりを使ってツールを構築したい。
Code Festival 2017 J (Tree MST) と 距離空間上のボロノイ図
春ですね。今回はCode Festival 2017のJ問題に対する面白い着眼点を紹介します。
問題はこちら -> J: Tree MST - CODE FESTIVAL 2017 Final | AtCoder 1900点!
ボロノイ図の説明はこちら -> ボロノイ図 - Wikipedia
想定読者層 :
- MSTを知っている人
- Kruskal法の適用中、頂点x,yを結ぶ辺が飛んで来たあと、それをMSTの辺として選んでも選ばなくてもその時点で構成中のMSTの辺のみを利用してxからyへ到達可能である、ということを理解している人
二次元空間上に点を配置した時の最小全域木(MST)のコスト
さて突然ですが、このサブタイトルの問題はどう解けるでしょうか。
やはり点の個数Nに対してO(N log N)程度で解けてほしい気持ちがありますが、
各点対間の距離を計算してしまうようではO(N^2)かかってしまいます。
いきなりですが、この問題の答えを言ってしまうと、
です。
つまり、下図の例ですと、全部で6組の点対のうち、左側の点と右側の点を結ぶ点対は領域が接していないため計算する必要がないということです。

二次元ユークリッド空間上でボロノイ図を構成するO(N log N)のアルゴリズムが存在することが知られていて(参考 : Fortune's algorithm - Wikipedia)、さらに、(こういうアルゴリズムが存在するなら当然)隣接する領域の組の個数はO(N)であることが知られている(参考 : ボロノイ図とその3つの性質 | 高校数学の美しい物語 )ため、 このMST問題はO(N log N)で計算できることになります。
やはりポイントとなるのは「ボロノイ図で隣り合っているところしか見なくてよい」というところに尽きます。なぜこうなるのかをざっくり下図を用いてスケッチします。

これから、d(x,y)でx,y間の距離を表すことにします。
上図では、点x,y をおき、その中点をa、 さらに点zをd(x,a) = d(y,a) > d(a,z)となるようにとっています。
ボロノイ図で領域が隣接していない点対x,yをとった場合、このようなa,zがとれます(厳密にはとれない場合もありますが、それは細かいので考えないことにします)。
d(x,a) > d(a,z)の両辺にd(x,a)を加えれば、
d(x,y) = 2 d(x,a) > d(x,a) + d(a,z) >= d(x,z) がわかります。
これはd(x,y)と d(y,z)の関係に対しても言えます。
すると、Kruskal法では点対(x,y)より点対(x,z), (y,z)のほうが先に評価されることがわかります。
こうなると、点対(x,y)を比較するころには(x,z), (z,y)が先に連結になっていることから(x,y) の間もすでに連結だとわかるので、Kruskal法でこの点対(x,y)は必ず棄却されることになります。
したがって、点対(x,y)の距離の情報d(x,y)がなくてもアルゴリズムの返す解に影響はありません。
2次元空間からグラフの空間へ
次の問題を考えましょう。
距離付きのグラフG=(V,E,w)とVの部分集合Uを用意します。
集合Uに含まれる2点x,yの距離d(x,y)をグラフG上でx,yを結ぶ最短距離とします。
頂点集合としてUを持つ完全グラフH=(U,E',d)におけるMSTの最小コストはいくつか?
(つまり、xyを結ぶ辺のコストをd(x,y) とするときのMSTを求める問題です )
この問題は、距離を定義する空間を2次元のユークリッド空間から指定したグラフGから作られる空間にしたとみなせます(言い回しが数学的には雑ですが勘弁してください)。
では、この問題にも先ほど紹介したボロノイ図を用いた解法を用いることはできるでしょうか?
答えはYesです。上で用いたボロノイ図の説明をそのまま使う方針で説明可能で、その際「中点」など、ユークリッド空間特有の表現を距離空間上の言葉に直せば適用できます。
この説明で網羅していないのはスターグラフのようなケースで、要するにある頂点が多くの領域の境目になっているケースです。
そうなると、それぞれの境目について点対の距離を計算したいため、頂点数の二乗個の辺をアルゴリズムに突っ込みたくなります。
しかし、このケースでも、任意の点対が同じ距離なだけなので、Kruskal法を実行する際には順番を気にしなくてよいです。
したがって、代表点とその他の点を結ぶ辺のみをアルゴリズムに放り込めばよいことがわかります。
以上の考察から、次のアルゴリズムを得ることができます。
(ただ、言葉だけだとなんとなくわかりづらいので、この問題はボロノイ図っぽくやって境目を見つけれてMST、でOKだと思って飛ばして問題ありません。実際次節に図があるので、それだとイメージをしやすいかと思います。)
- プライオリティーキューに、Uに含まれる頂点と距離0の情報を挿入します。このキューの順序は距離で付けます。
- キューが空でない限り下のことをします
- キューから距離が一番小さい頂点vを選んで、キューからpopします。
- 頂点vに対して、まだ以下の説明にある隣接頂点を見ていく処理をしていないなら、その距離とU上のどの頂点から来たかを記録し、以下のように隣接頂点を見ます。
- 隣接頂点uを見て、これがすでに記録されているなら、頂点uに登録されている頂点と頂点vに登録している頂点の距離を、(uに記録された距離) + (vに記録された距離) + 辺v,uの距離として、Kruskal法で使うコスト情報として登録します。
- 隣接頂点uが記録されていないなら、これをプライオリティーキューに挿入します。このとき、vに記録した距離に(v,u)の距離を足したものであること、Uのうちどの頂点から来たかを伝えます。
- Kruskal法を動かす
このアルゴリズムはグラフGの頂点数Nと辺数Mに対して、だいたいO( ( N+M) log (N+M))程度で動作し、Kruskal法のために登録する辺数もM程度で抑えられるので、頂点集合Uのサイズが膨大でも動作します。
Code Festival J, Tree MST
本題に戻ります。しかし、ここまでの説明を読めば、この問題はかなり簡単ではないでしょうか。
というのも、TreeMSTで定義されている距離をグラフを用いて書いてみると以下のようになります。(この図は本家問題文の例1に対応しています)
前節の説明で頂点集合Uに相当するのが、1,2,3,4と黒字で番号がついている頂点の集合で、Vは1',2',3',4'を加えた8頂点からなる集合になります。

このようなグラフの作り方で、「頂点 u から頂点 v までの距離」と「Xu+Xv」の和、という距離をグラフで自然に表現できます。
これにボロノイ図的な考え方を適用すると次の色分けができます。

これで全域木に登録される辺の候補は、領域の境目となっている(1,2), (1,3), (1,4) でよいことがわかるので、コストは(1+1+3) + (1+1+2+5) + (1+1+2+3+1) = 22になることがわかります。
( UPD 19/1/14 補足・この上の色分けの図の直感的な説明は kobaeさんの説明
KEYENCE Programming Contest 2019 E - Connecting Cities - koba-e964の日記がわかりやすいです:
- 頂点1, ..., Nから色1, ..., Nの液体が同じ速さで流れ始める
- 色の違う液体は触れると触れた場所がその場で固まり、互いに混じり合わない。触れた場所以外はそのまま流れ続ける。
- 最終的に全ての液体の動きが止まった時の液体の配置がヴォロノイ図である
そもそもボロノイ図はその定義から、以下動画のように、
各頂点からこのように色を広げていって、最終的にできる図形である、ということになります。
www.youtube.com
www.youtube.com
これと同様のことをグラフでやろうとすると、最初は頂点集合Uに含まれる頂点に異なる色を塗り、
それ以外の頂点が何色で塗られることになるのか調べることになります。
その結果、上の色分けになります。
また、これを行うために、ダイクストラ法のような実装になります。
)
このように、ちょっとオーバーキル気味ですが、ボロノイ図的な方針で解くことができます。
コードは Submission #1818510 - CODE FESTIVAL 2017 Final | AtCoder ここにあります。短いですね。(なお、とくにこの問題では領域の境目の個数がちょうどN-1個になりますので、Kruskal法を使う必要はありません。)
また、この着眼点から考えると、TreeMSTの元となるグラフを木でなく、一般のグラフに拡張しても自然に解けることがわかる点も面白いです。
類題
(UPD 19/1/14 ) KEYENCE Programming Contest 2019 E - Connecting Cities
Tree MSTの部分問題です。
snukeさん紹介の問題
20桁の二進数のうちN個が与えられます。これを頂点とし、各頂点間に2つの二進数のハミング距離をコストとした完全グラフにおけるMSTを求めて下さい。
— ꑄ꒖ꐇꌅꏂ (@snuke_) 2018年3月24日
自然にこれも解けますね(Judgeがどこにあるかわかりませんが)。
JOI 春合宿 2014 Day2 水筒
(HIRさんに教えていただきました。ありがとうございます!)
目標は違いますが、アイデアはよく似ています。
JOI 2013/2014 春季トレーニング合宿 課題
この方針が適用できない問題
今回紹介したボロノイ図的な考え方は、ある距離行列が与えられたとき、これを適切なグラフに埋め込んで表現できる場合に適用可能です。
したがって、次のような問題には適していないと思います。https://csacademy.com/contest/round-72/task/rectangle-mst/
この場合はこの距離行列を特定のグラフに埋め込むことができそうにありません.....
Project Selection (燃やす埋める) 周りの話についてもう少し考えた
Competitive Programming Advent Calendar 2017 - Adventar アドベントカレンダー最終日です。
先月はこの過激記事をご覧になった方も多いのではないでしょうか。 : 『燃やす埋める』と『ProjectSelectionProblem』 - とこはるのまとめ
これについてもう少し色々な視点から整理したり、最近考えていた拡張を書いていきます。調査が不十分な点・誤植もあるかと思いますが、ご容赦ください。(誤植は教えていただけると助かります)
以下、Project Selection Problemは略してPSPとしておきます
また、前回の記事周りの話はそんなに面白くないので後回しにします。
拡張を考えていた話
モチベーション
私はPSPの信者なので、できるだけこれをサブルーチンとして利用することで、いい感じに問題を解きたいです。
しかし、イマイチ使い方がわからない問題があります。それが https://www.codechef.com/DEC14/problems/RIN この問題です。
想定解法では、面白いグラフの張り方をしています。知らない方はこの問題のeditorialをご覧ください。
ただ、今後紹介する方針ではなく、editorialにあるグラフの方が綺麗だと思います。
拡張
この問題をなんとかPSPの枠組みで解けるようにするために、PSPに対して次のような拡張をします。
プロジェクト i は集合 0,..., K-1 のうちのどれかの値が割り振られるとします。
このとき、p[i,0], ..., p[i, K-1] だけの利得がそれぞれ得られます。簡単のため、p[i, 0]=0とします。また、プロジェクト i に k 以上の値を割り振れば プロジェクト j に t 以上の値を割り振らないと コストcが発生します。
プロジェクトに値を割り振ることで利得を最大化せよ。
これは一つのプロジェクトあたり、次のような利得と関係をつけたグラフをつけると表現できます。
矢印はINFコストを表現します。

一番左が選ばれるとその右がすべて選ばれるため、合計の利得はp[K-1]とみなせます。一番左を選ばず、その右が選ばれると合計利得はp[K-2]になります。どれも選ばなければ0( = p[0])です。このようなグラフを用意することで上記の拡張でも表現できることがわかります。
では、上記RINを解くときにはどうなるのか。必要なものは講義xの後に講義yを取る条件を入れ込むことです。
これは「講義xがk以上なら、講義yはk+1以上である。」という条件を各semester kに入れれば表現できます。
つまり、次のようなグラフを作るのがざっくりした方針になります。

細かいことを言うと、開講されていないsemester などを考慮する必要があるので、そういう頂点は利得を -M(Mは十分大きい定数)とする
などの工夫が必要と思います。その点で、想定解法より汚くなるかもしれません。
ただ、想定解法とは異なるグラフが構成できることは非常に興味深いです。
さらなる解釈
このような一般化PSPは次のことをしているとも思えます。
A[K-1] ⊂A[K-2]⊂ ... ⊂ A[0] であるときに、点x を 集合A[0]内に配置する。
点x をおいた場所が x ∈ A[i] ならq[i]点を獲得するまた、x が A[i]内にあるとき、 y はA[j] 内にいなければ c 点減点される。
これを見ると、集合の切り分け方が部分集合関係の鎖になっていることが本質的な気がしてきます。
そこで、次の問題を考えてみましょう。
3状態へ割り振るタイプの問題
これと関連して問題を1つ。「i番目のものを埋めるとxi円、燃やすとyi円貰えます(xi,yi>0)が、何もしないということもできます。i番目のものを埋めてj番目のものを燃やすのは駄目というペアがいくつか与えられます。もらえるお金を最大化してください」さて、どうやってグラフを作りますか?
— SKY/sky58 (@skyaozora) 2017年11月13日
いくつか前の記事でも登場しましたが、この問題で前節で紹介した切り分けが重要であることを確認します。
この問題が初見であれば、次のように、「燃やす集合」、「埋める集合」といった集合をそれぞれ作るアプローチを取るところから始めるのではないでしょうか。
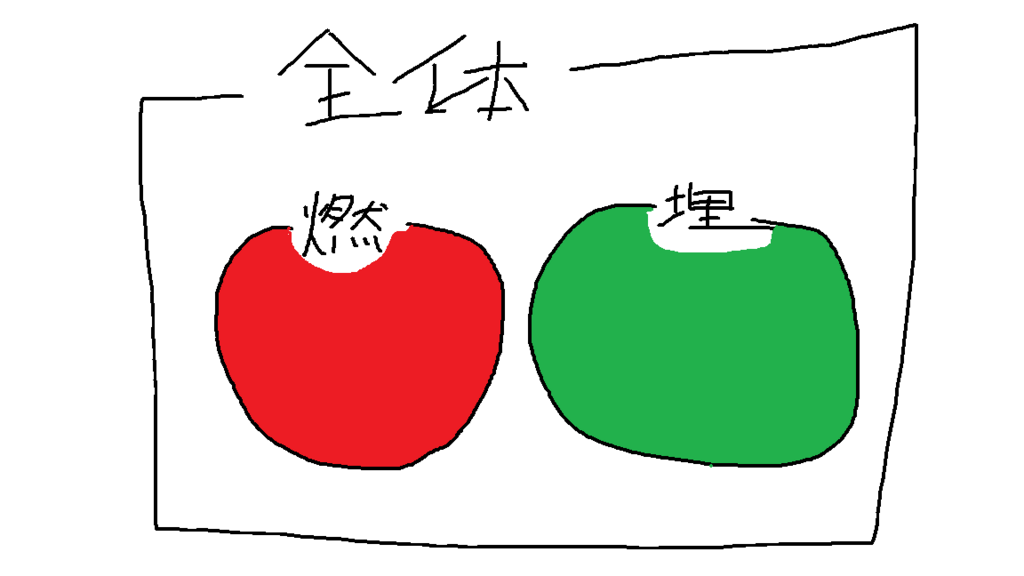
実際こういった気持ちでスタートしてもPSPを構成できます(参考 : 続:『燃やす埋める』と『ProjectSelectionProblem』 - とこはるのまとめ)が、片側の状態の01を反転する必要が出るため、なんだか奇妙でした。
しかし、先述した部分集合の鎖で考えることが自然だと思うと、次のように層を分けるのが自然そうに見えます。

つまり、(燃やす) ⊂ (埋めない) ⊂(全体)の関係です。
入れたい条件は、「xを燃やすならyを埋めない」の関係だったので、制約もちゃんと入れることができることがわかります。
TCO2017 Semifinal2 500 RatingProgressAward
これも何件か前の記事で紹介しました。(詳細は TCO2017 Semifinal2 500 RatingProgressAward - とこはるのまとめ)
この記事を参照すると、問題の言いかえは次のようなものでした。
ProjectをN個用意し、それぞれのProjectは proj[i]=0,1,2のように3値をとれるものとします。
このとき、a[i]からb[i]に到達可能ならproj[a[i]] >= proj[b[i]]を満たさなければならないとき、
proj[k]==1となるProject kに関して、change[k]の総和を最大化せよ。
この問題での集合の切り分けはproj[k] >= 2, proj[k] >= 1 とわけることが自然でしょう。
まず、「proj[k]==1となるProject kに関して、change[k]の総和」は
proj[i] >= 1ならchange[i]を足し、proj[i] >= 2ならchange[i]を引けばOK。
次に「a[i]からb[i]に到達可能ならproj[a[i]] >= proj[b[i]]」は
proj[b[i]] >= 1 ならば proj[a[i]]>=1,
proj[b[i]] >= 2ならば proj[a[i]] >= 2の制約を入れればOKです。
これだけわかれば解けてしまいます。
これでかなりお手軽に解けるようになったのではないでしょうか?
前記事の感想などを見て
色々思ったことを書きます。
前記事においてPSPの有用性を主張していました。
意図としては、
- より思考をショートカットできるしお手軽な道具じゃないか?
- ちゃんとこの辺りのテクにはそういう名前がついている
の周辺の2点を主張していたつもりでした。
これについて共感してくれる人が少なかったのはかなりショックでした。
ただ、この二点については考え始めるとどっちでもいいのかもという気持ちになってきました。
後者の名前は、twitterや会話における意思疎通において、解法のスケッチを伝える上で「燃やす埋める」は大変便利です。だからこれからも残り続けるでしょう。
ただ、PSP側も何か調べものをする意味で覚えておいて損はないとは思っています(マージテク <-> weighted union heuristics の関係に似ていると考えています)
前者のテクそのものとしての有用性は個人的には
- 適当にグラフを作ると後からグラフを変形する可能性があるという点
- 最大流の結果との定数を足し引きする整合性を管理するのが面倒
という二点が気がかりでした。
両方の懸念も、考え方に慣れればどうでもよさそうです。
個人的には最初はPSPの手順そのままに考えればミスも減るし入門として適していると考えてはいますが。
そもそも論として、強い言葉を使いすぎたのはまずかったです。
それから、skyさんのこのツイートにはかなり救われました。この場で感謝いたします。
自分が燃やす埋めるだと思ってたものはProjectSelectionProblemと呼ばれているものだったらしい(これDPとメモ化再帰とか、配るDP貰うDPみたいな感じで両方の感覚を身に着けておいて損はないのでは 『燃やす埋める』と『ProjectSelectionProblem』 - とこはるのまとめ https://t.co/W6YiJaY0sN
— SKY/sky58 (@skyaozora) 2017年11月13日
最後に
この辺りの最大流のグラフの作り方は必ずしも一通りではないケースが多いと認識しています。綺麗なグラフで解けている場合もあれば、意味不明なグラフで解いているケースもあり、解答者が何を考えているのかわからないこともあります。
いろんな人がこの問題に興味を持てば色々な解釈がわかって面白くなる気がしています。実際、次の記事は私の一連の記事のあとに公開されました。最後の例が面白いです。
最小カットとProject Selection Problemのまとめ · うさぎ小屋
ところで、これは今回の話と無関係ですが、私は競技プログラミングに対して真っ当な努力はできていないので、今年のAdvent Calendarの記事も大変助かっています。今年も雰囲気でしか知らなかったテクをちゃんと知ることができて大変有益でした。多分世の中ガチ勢ばかりではなく、私みたいな人はたくさんいると思うので、来年のAdvent Calendarでも記事を書いてほしいです!
みなさんよいお年を!
第2回ドワンゴからの挑戦状「花火」に対するシンプルな解法と最小費用流の双対
競技プログラミングアドベントカレンダー2017(その1)の二日目の記事です。
adventar.org
この記事では花火に対するシンプルな解法を説明します。これは最小費用流の双対問題を用いて説明できますので、そういったことに触れつつ解説します。本文は次のPDFに書きました。 http://tokoharu.github.io/tokoharupage/docs/advent2017.pdf
面白いポイントとしては、このテクを用いれば UTPC2012の"じょうしょうツリー"もかなりシンプルに書ける点だと思います。じょうしょうツリーについてはその解説では meldable heap を用いるというのが想定解法でしたが、今回紹介する方針でやればかなりシンプルにかけるかと思います。
そのほか
- tikz を使ったけどハマったときに結構苦労するなぁ
- Project Selection Problemの件はちょっと待ってください。
TCO2017 Semifinal2 500 RatingProgressAward
(UPD 12/24) 説明に誤りがあったので修正。
前回の続きです。
前回はいろはちゃんの疑問に答えたつもりでしたが、聞いてみたところ違った問題のことを指していて、表題の問題だったようです。
link :TopCoder Statistics - Problem Statement
今回もProjectSelectionProblemを経由して解いていきたいと思います。
問題概要
- 授業をN課程とります。
- 順番は任意でよいですが、1課程ずつ順番に受講しなければなりません。
- 課程b[i]を受講するためには、すでに課程a[i]を修了している必要があります。
- 最初のレーティングは1200です。
- 課程iを受けるとratingが += change[i]だけ変動します。
- k個の課程受けた直後のratingをv[k]とします。k=0なら初期値です。
- このとき、Rating Progress を max( { v[i] - v[j] | i > j } )と定めます。
- 受講する課程の順番をうまく選ぶことでRating Progressのありうる最大値を求めよ。
解法
問題の言いかえ
この問題はある種のProjectSelectionProblemっぽくみえます。「ぽい」と表現した理由は、次のような問題に言い換えてProjectを定めることはできるものの、ProjectSelectionProblemのフレームワークに適用できない形だからです。
ProjectをN個用意し、それぞれのProjectは proj[i]=0,1,2のように3値をとれるものとします。
このとき、a[i]からb[i]に到達可能ならproj[a[i]] >= proj[b[i]]を満たさなければならないとき、
proj[k]==1となるProject kに関して、change[k]の総和を最大化せよ。
これをどうにかProjectSelectionProblemに適用しようと思っても、「ならば」の制約がうまく入らないためどうにもうまくいかなさそうです。この「ならば」がうまくいかないのは1,2の間の「ならば」と0,1の間の「ならば」が共存できないことに由来しそうなので、この二つの制約を分離することをこれから考えていきます。
Projectの定義
その結果、次のような2N個のProjectを作ってみることにします。
最初のN個 :
- B(ベース)に属する <=> 0に属する
- Aに属する <=> 1,2に属する
残りのN個 :
- B(ベース)に属する <=> 0,1に属する
- Aに属する <=> 2に属する
ただし、それぞれの種類のProjectで、最初からi番目が課程iに対応するものとします。
最後に得たい答えの求め方
このとき、どうすれば1に属する利得を計算できるかですが、最初のN個でAに属するProjectと、残りのN個でBに属するProjectのchangeの総和を足し、最後にchange[i]の総和で引けばよいです。(ちょっとトリッキーですね)
制約
次に制約を考えます。考える制約は二種類です。
- 課程の順序制約
これはb[i]がAに属すればa[i]がAに属す制約でよさそうです。だからフロー用グラフにb[i]からa[i]に∞容量の辺を張ります。この制約はどちらの種類でも共通です。
- 2つのプロジェクトの整合性制約
本来1つのProjectと扱いたいものを2つのProjectに分離しました。ここの整合性がとれていなければいけません。具体的には、前者でBに属し、後者でAに属している場合に0かつ2に属して矛盾となるためこれを避けたいです。したがって、後者のプロジェクトがAに属している場合に前者のプロジェクトはAに属している必要があります。だから N + i からiに∞容量の辺を張るような感じになります。
利得
次にProjectSelectionProblemの構成要素として利得があるのでこれを考えます。
これはBに属しているときから見た、Aに属したときの相対的利得になります。
最初のN個はBにいるときにchangeをカウントせず、Aにいるときにchangeをカウントしたいです。だから最初のN個の利得pはchangeそのままです。
一方、後のN個はBにいるときにchangeをカウントし、Aにいるときにchangeをカウントしません。だから後のN個の利得pは正負が反転して-changeになります。
ここまでで最大流のグラフを作り終えることができました。
最大流を除いた部分の整理
最後に、最大流の外側で計算する部分について整理します。
- ProjectSelectionProblem内部での総和部分
これは利得のうち、正であるものの総和なので、 abs(change[i])の総和になります。
- ProjectSelectionProblemのBに所属させる際に発生する利得。
これは後者のProjectで発生します。これはchange[i]の総和です。
- ProjectSelectionProblem外部でもともと解きたい問題の答えを得る。
これは以前説明した通り、change[i]の総和を引きます。
これら3つを合計することで、 abs(change[i])の総和を事前計算しておけばよく、結局 sum(abs(change[i])) - maxflow(s,t) が答えになります。
コード
以上のまとめとして、ACしたコードの一部を載せます。max_flowのライブラリを持っていると仮定し、add_edge(v,u,c)はフローを流したいグラフに対してvからuへ容量cの辺を張ることを指します。
int RatingProgressAward::maximalProgress (vector <int> change, vector <int> a, vector <int> b) { int N = change.size(); int ans = 0; int s = 2 * N, t = s + 1; for(int i=0; i<N; i++) { ans += abs(change[i]); add_edge(i+N, i, INF); if(change[i] > 0) { add_edge(s, i, change[i]); add_edge(N+i, t, change[i]); } else { add_edge(s, N+i, -change[i]); add_edge(i, t, -change[i]); } } int M = a.size(); for(int i=0; i<M; i++) { add_edge(b[i], a[i], INF); add_edge(N + b[i], N + a[i], INF); } int ret = max_flow (s,t); return ans - ret; }
個人的には割ときれいなグラフだと思っています。
本番でACされたコードを貼っておきます(要Login)。
tourist https://community.topcoder.com/stat?c=problem_solution&rm=330662&rd=17017&pm=14719&cr=22263204
ikatanic https://community.topcoder.com/stat?c=problem_solution&rm=330662&rd=17017&pm=14719&cr=22711754
全く違いますね。ちゃんと読めていないのでわからないですが、もっと簡単な考え方もあるのかもしれません。何かご存知の方がいらっしゃれば教えていただけると幸いです。
コメント
こうして出されてみると難問でしたが、考察の流れを考えれば拡張が容易にできそうにも見えます。
というのも、今回は 2 > 1 > 0にわけた領域のうち、それぞれの利得の重みを0,1,0としたような問題でしたが、これはp,q,rみたく係数をつけて一般化できそうに見えます(本当にできるか未チェック)。
こういう想像が働くようないい感じの解が得られて割と満足です。